Abaqus tosca tutorial - assured
In the current blog we will show some capabilities of one of Simulia’s extended products, Tosca. As a quick recap, based on your license you can use your tokens to run Simulia Abaqus or you can also use your licenses to run products of the extended portfolio:
- Abaqus (Finite Element Analysis)
- Fe-Safe (Fatigue Analysis)
- ISight (Parametric Optimization)
- Tosca (Non Parametric Optimization)
Non parametric optimization
We will focus on Tosca which is a tool for non-parametric optimization. Contrary to I-Sight which is a parameter based optimization tool in Tosca a general design space can be created and based on the requirements the software will determine a natural shape that can carry the necessary loads at a minimum weight-expense. In Tosca as long as some criteria is satisfied then the shape will be freely defined inside the domain defined as designed space. On the other hand in I-Sight the parameter(s) must be identified, therefore it should be something that already exists, such as a diameter, a radius, a thickness, a Young’s Modulus, etc.
In the current blog we will show a non-parametric optimization performed on Simulia Tosca. The product that we will optimize is a skateboard truck, see Figure 1. The skateboard truck was drawn natively in Abaqus and is therefore a simplified representation, Figure 2. However, it can fully show the goal of starting with a gross design and let the software help you to have a new design that hardly would have been the first iteration in the design process. For the simulation the truck is fixed in the areas where the screws are placed and is loaded vertically in the areas of the wheels representing the reaction of the ground when a person stands on the board.


Figure 1.- Skateboard, left and un-mounted skateboard truck with wheels, right.
When doing optimization the goal is to define the possible stiffest part at the lowest amount of material (with a fraction of the initial volume). Thus, removing material while still having a part that can withstand the design loads is much what this process is about. Therefore, you can think that you need to have a generous volume where material will be removed and you will end up with a product that can be close to the final design. That is the reason why the parts drew in the truck, Figure 2, are big and thick in comparison with that from Figure 1 right.


Figure 2.- Initial design of the skateboard truck.
Define the design space
Step by step in an optimization process you need to create an optimization task and define the design space, Figure 3. In this case we defined everything as the design space, thus, in principle, material can be removed from every region in the model.

Figure 3.- Creating an optimization task and selecting the whole model as design space.
Define design responses
Then, a design response needs to be created. We have created a design response for Energy stiffness measure and another design response was created for the volume, Figure 4.
Figure 4.- Creating a design response for Energy stiffness measure and for volume.
Create objective functions
The design response for energy stiffness measure will be minimized by creating an Objective function, this will produce the stiffest possible solution, Figure 5.

Figure 5.- Objective function to minimize the energy stiffness measure.
Create optimization constraints
With the other design response (volume) we will create a constraint so that the response is limited to a certain percent of the initial volume, Figure 6. The volume is related to the mass of the system which we are trying to minimize.
Figure 6.- Constraining the final response to a fraction of the initial volume.
Creating geometric restrictions
Initially we have defined the whole model as part of the design space but some areas cannot be redesigned, for instance the holes for the bolts/screws and the external sides of the axle where the wheels should be mounted, highlighted in red in Figure 7. This restrictions can be considered and under Geometric restrictions. Other type of geometric restrictions not considered here could be, demold control, planar control, rotational symmetry, cyclic symmetry, point symmetry and member size. The latter was also prescribed to control the size of the members, sometimes the software can create thin or thick members that later on represent problem during the manufacturing process.

Figure 7.- Frozen areas where material cannot be removed.
Finally, it is time to create an optimization task and define the maximum number of iterations to be performed. In the current analysis we have performed 30 iterations, Figure 8.

Figure 8.- Creating an optimization process and defining the number of iterations.
Optimization results
The resulting iterations are shown in Figure 9. It can be seen how material is being removed until it ends with the most efficient solutions in terms of maximum stiffness and volume reduction. Figure 10 shows the final shape and the resulting stresses for the design load.


Cycle #2


Cycle #5


Cycle #12


Cycle #19
Figure 9.- Optmized part throughout the optimizing cycles.


Figure 10.- Stresses in the optimized part
As it can be seen the bottom part of the skate truck was the one where most of the optimization took part. It could be that the design was far away form a final design and therefore there was plenty of room for improvement whereas for the top part, that contains the axle, the design was close to the end product and so it did not have a lot of extra material where optimization could be performed, perhaps something to consider for a following optimization run. Do you have access to Abaqus and Tosca and would like to give it a try yourself? Feel free to request the files.
Extract the geometry to a CAD environment
Finally, the optimized part can be fine-tuned in your CAD environment; i.e. the areas where the screws/bolt heads need to rest can be flatten. A .stl file can be extracted and imported in SOLIDWORKS for instance, Figure 11.


Figure 11.- Extracting the final shape and importing in SOLIDWORKS
Would you like to know more about optimization?
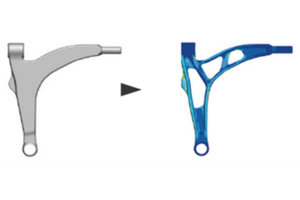
Tosca Structure provides topology, shape, sizing and bead optimization for mechanical structures based on simulation results from industry standard FEA packages. These methods accelerate and improve the reliable design of lightweight, rigid and durable components and systems. In addition, including optimization in your product design cycle has the potential to significantly reduce the required number of expensive improvement loops and prototypes.
This course is a comprehensive introduction to the structural optimization capabilities of Tosca Structure:
- Solving fundamental topology, shape, sizing and bead optimization problems
- Results evaluation
- Integration of optimization into the development process
- User interfaces for an efficient workflow
The topics covered include:
- Introduction to structural optimization with Tosca Structure
- Optimization workflow in different user environments (Tosca ANSATM environment, Tosca Structure.gui, Tosca Extension for ANSYS Workbench)
- Getting the best structure: topology optimization with Tosca Structure.topology
- Effective and quick evaluation: Visualization, postprocessing and result validation
- Improving durability, stress reduction, increasing frequencies: shape optimization with Tosca Structure.shape
- Optimal design for sheet metal structures: shell thickness optimization with sizing
- Maximizing stiffness of sheet metal structures: bead optimization with Tosca Structure.bead
- Integration of Tosca Structure in your development process: Interaction with FE-Solvers and result transfer for CAD
This seminar is recommended for all new Tosca Structure users, independent of the FE-Solver and Pre-/Postprocessing environment in use. Participants should have some basic knowledge of CAE in order for the course to be effective. Experience with structural optimization techniques is not required, however.
Course Overview
The overview provides details of the topics covered in each lecture. Please note that the actual course agenda may vary depending on location.
- Click here to view the schedule
eLearning
Click here for a complete listing of Tosca classes on the 3DEXPERIENCE Edu SPACE platform
Tosca struct-book
Bird strike Simulation helps in assuring aircraft safety, in eliminating cost & effort required for practical tests. There has been significant research done on various ways of doing bird strike simulation, till date Aerospace & defense Industry is concerned with two key issues 1.Comparative assessment of available methods 2. A FE model for fastener failure and fastener hole embrittlement. Current paper addresses relevant issues for today’s industry towards a universally accepted method of bird strike analysis Finite element based computational methods. First part of current research aims at bring out comparison between analysis methods along with their pros and cons, the Explicit analysis capabilities of Abaqus were used for modeling the phenomenon using three methods LAGRANGIAN, COUPLED LAGRANGIAN-EULERIAN (CEL) and SMOOTH PARTICLE HYDRODYNAMICS (SPH). Results are compared with published literature based on the standard experimental data. Critical parameters like HUGONIOT pressure and Stagnation pressure are compared from each study. Merits in all the three methods and bird models are presented with a view to guide the user in choosing an appropriate method depending on time and resource availability. A first of its kind Bird Strike Simulation Index (BSSI) proposed with FEM setup time, run time and accuracy as parameters, BSSI will be a holistic guidance for industrial user. Second part of the paper deals the most challenging issue of fastener modelling for dynamic loads. Analysis of bird impact modeling onto metallic riveted panels, which are typically idealized models for many practically used airframes structures like wing, flap, trailing edge, leading edge, are done using pure Lagrangian and SPH method. In high velocity bird strike scenario, fasteners will experience both shear and tensile loads and failure of aircraft structures are also governed by fastener failure modes. The fasteners behavior is modeled to simulate the failure due to shear load, tensile load and combined loads. Tensile and shear damage modes are simulated by supplying stiffness values in all connectors. This was possible because large variety of fastener modeling methods available in Abaqus. Results are in good agreement with published experimental results. In reality aircraft components usually contain large number of fastener holes which will significantly define the failure behavior of components of assembly due to micro level embritlement around fastener hole. A first of its kind methodology for fastener hole and fastener damage is implemented which could successfully interlinked to the global impact failure with local micro embritlement
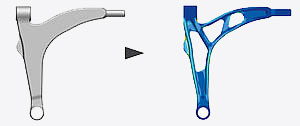
Tosca Structure is the market leading technology for structural optimization based on the industry standard finite element analysis (FEA) package Abaqus, to create innovative and sustainable designs. From early conceptual design through to detailed design improvements Tosca Structure offers the full range of optimization solutions:
- Tosca Structure.topology
- Tosca Structure.sizing
- Tosca Structure.shape
- Tosca Structure.bead
- Optimization module in Abaqus/CAE
- Tosca Structure.gui
- Economic use of existing IT investments
- Faster turnaround from analysis to design or manufacturing
- Less prototypes or right the first time
- Accelerated product development for a shorter time-to-market
- More durable and lightweight designs
- Optimized products drive innovations in your market
- Seamless integration with leading FEA & durability solvers
- Direct use of existing knowledge and models
- Full design flexibility without time-consuming parameterization
- Fast and easy creation of design variants avoiding intermediate CAD modifications using shape morphing capabilities
- High fidelity optimization for nonlinear analysis and durability
- Simultaneous optimization to meet static, dynamic, and thermo-mechanical requirements
- Handling of complex manufacturing conditions
- Automatic validation analysis runs and direct data transfer to CAD systems with selected graphical user interfaces

In the past, we have already given an example of optimizing a structure using Tosca. Now, I want to revisit this topic and focus specifically on geometry issues. I’ll explain how I obtained the geometry used for optimization, and also show how to get a 3D model of the optimized geometry, that can be used for further finite element analysis.
The example: a hip implant
Though we probably don’t always realize it, we use our hips a lot. After years of loading, they can become damaged and painful. In these cases, replacing the hip with an implant can be a solution. Here we are going to let Tosca design an optimized hip implant, as an example.
Topics: Abaqus, Topology Optimization, SIMULIA Tosca
Related Videos
#drilling process step by step using #abaqus ';} ?>
';} ?>
0 Comments